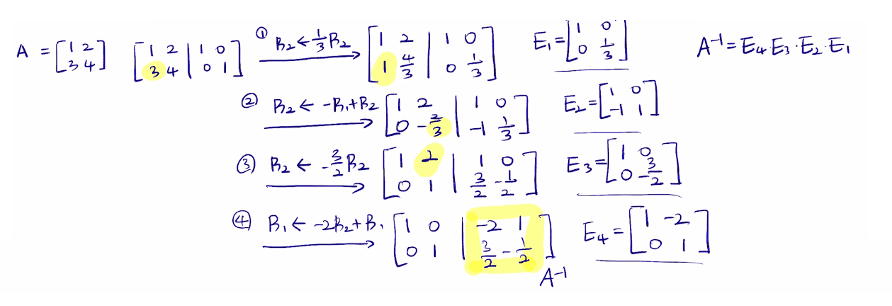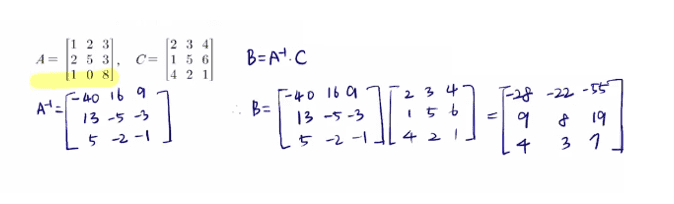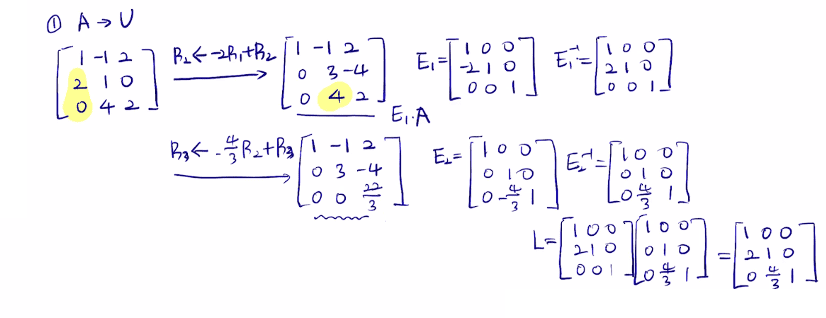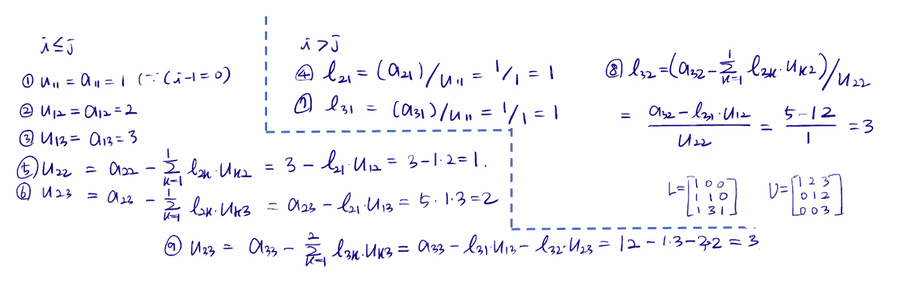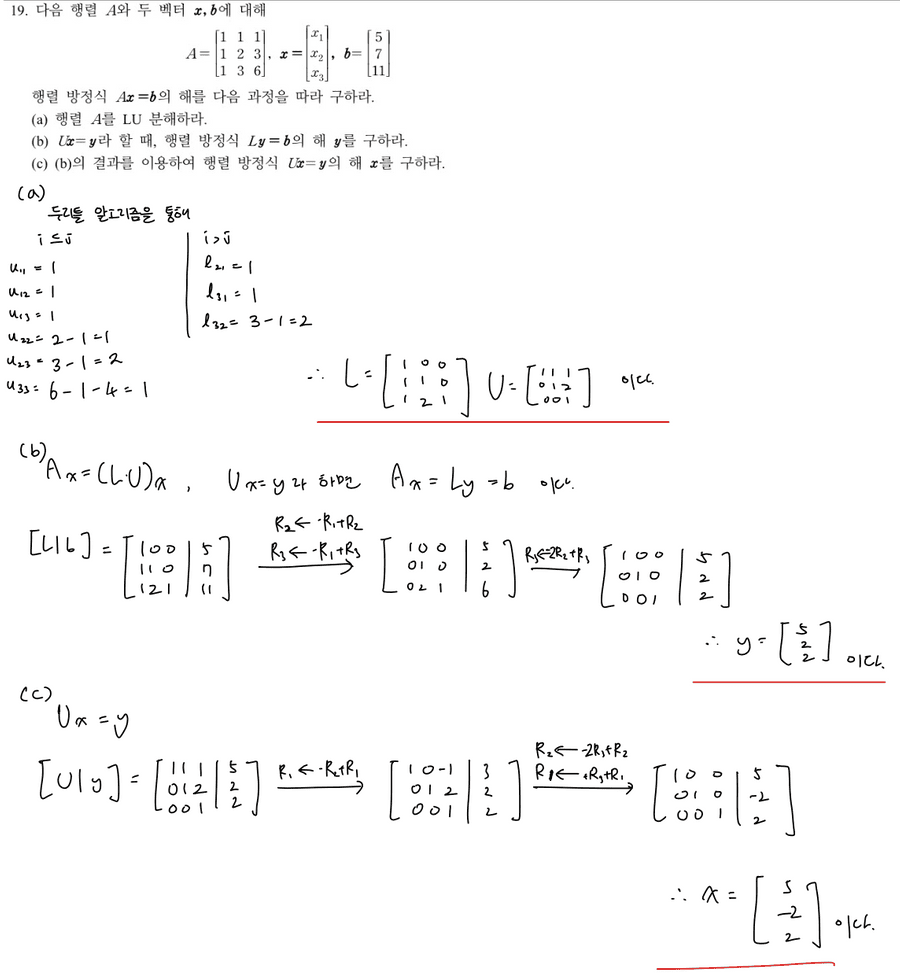기본행렬
📌 기본행렬(Elementray matrix)
단위행렬의 두 행을 교환하거나 한 행에 0이 아닌 상수를 곱사거나, 한 행의 상수배를 다른 행에 더하여 만든 행렬을 기본행렬이라 한다.
 기본행렬
기본행렬
- E1: R1 <=> R2
- E2: R3 <= 5R3
- E3: R3 <= −4R1+R3
📌 기본행렬의 특징
📌 행 동치(Row equivalence)
행렬 A, B에 대해 A를 B로 바꾸는 일련의 기본 행렬이 있으면 A, B는 행 동치라고 하며, A~B로 표기한다.
B=EnEn−1 ... E1A
위의 식에서 B가 단위행렬이라면 EnEn−1 ... E1은 A의 역행렬이 된다.
📌 기본행렬을 통한 역행렬 구하기
위의 식을 이용해서 첨가행렬(Chapter 2참고)로 역행렬을 구하는 행렬 방정식을 써보면
[A ∣ I] => [EnEn−1 ... E1A ∣ EnEn−1 ... E1] => [I ∣ A−1]
예제를 통해 2차 행렬과 3차 행렬의 역행렬을 구해보자.
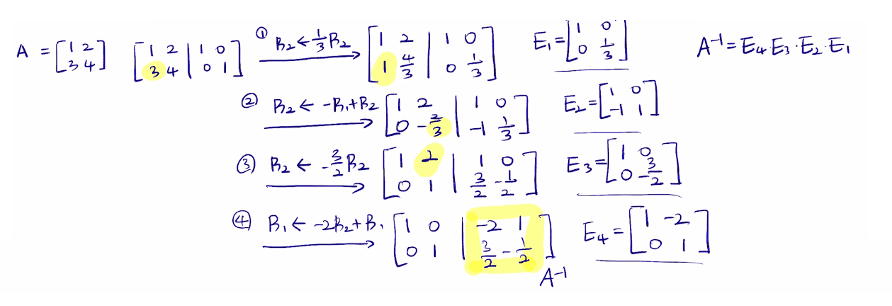 2차 행렬의 역행렬 계산
2차 행렬의 역행렬 계산
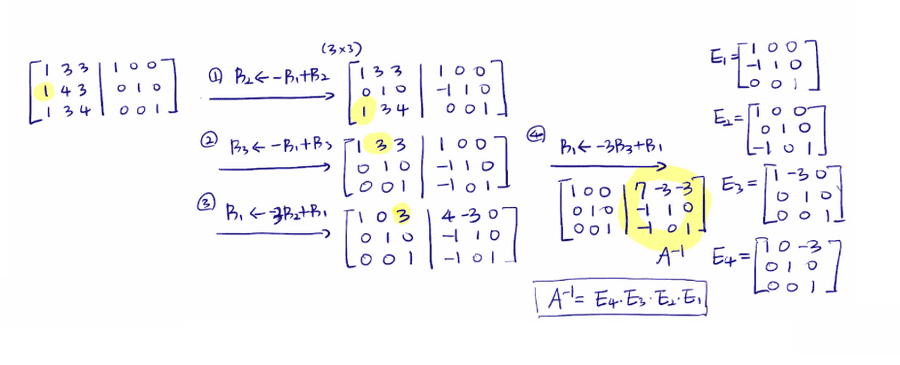 3차 행렬의 역행렬 계산
3차 행렬의 역행렬 계산
역행렬의 활용
📌 연립선형방정식 풀이
연립선형방정식을 나타내는 행렬방정식 Ax=b에서 A가 가역인 n차 정방행렬이고 b가 n×1 행렬일 때, x=A−1b는 유일한 해이다.
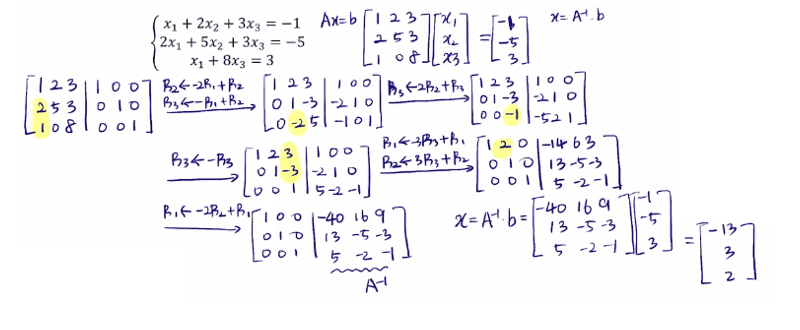 역행렬을 활용해 연선방 풀기
역행렬을 활용해 연선방 풀기
📌 행렬 방정식 풀이
연선방 풀이와 비슷한 방법으로 아래의 행렬 방정식도 풀 수 있다.
AB=C일 때 양 변에 A−1을 곱해서 B=A−1C로 구한다.
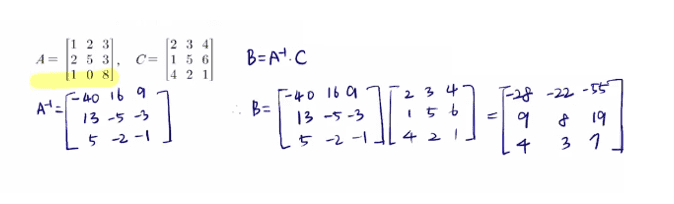 역행렬을 활용해 행렬 방정식 풀기
역행렬을 활용해 행렬 방정식 풀기
📌 동차 연립선형방정식(homogeneous system of linear equations)
Ax=0형태의 연립선형방정식을 동차 연립선형방식 이라고 한다.
⎣⎢⎡1322−13131⎦⎥⎤⎣⎢⎡x1x2x3⎦⎥⎤=⎣⎢⎡000⎦⎥⎤
x1=x2=x3=0
연립선형방정식의 경우 [해1개, 불능, 부정] 3가지 경우가 있는데, 동차 연선방의 경우 해가 1개인 경우 즉, x=0인 경우 자명해(trivial solution)라 하고, 부정인 경우 x=0인 해를 비자명해(non-trival solution)이라 한다.
동차 연선방 Ax=0에서 A가 가역이라면, 자명해만 존재하고, 미지수의 개수가 선형방정식의 개수보다 많은 동차 연선방에서는 비자명해를 갖는다. 비자명해인 경우와 자명해인 경우를 예시를 통해 살펴보자
ex1) ⎩⎪⎪⎨⎪⎪⎧x1+x2+x3=02x1+3x2+2x3=03x1+8x2+2x3=0
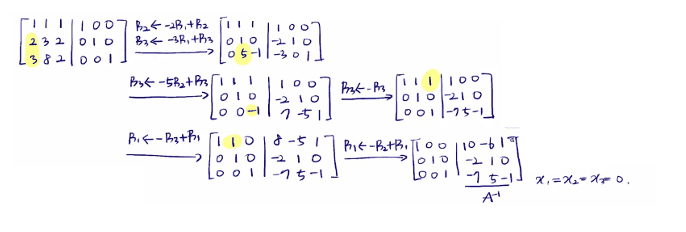 자명해를 갖는 경우
자명해를 갖는 경우
ex2) ⎩⎪⎪⎨⎪⎪⎧x1+x2+x3−x4=0x1+x4=0x1+2x2+x3=0
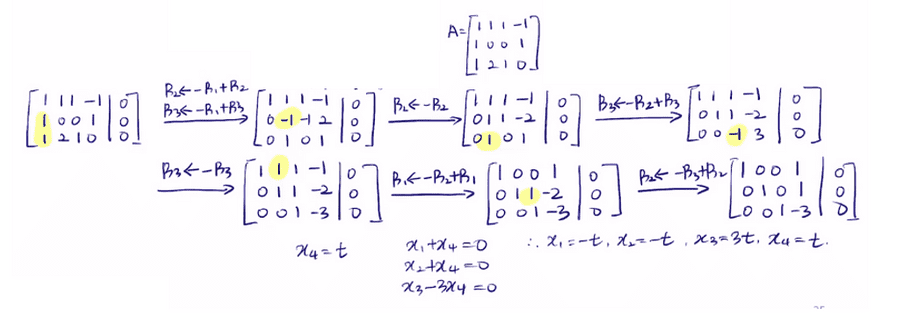 비자명해를 갖는 경우
비자명해를 갖는 경우
LU분해
📌 LU 분해란
임의의 행렬 A를 하삼각행렬 L과 상삼각행렬 U의 곱인 A=LU로 표현하는 것을 LU분해(LU 행렬 분해)라고 한다.
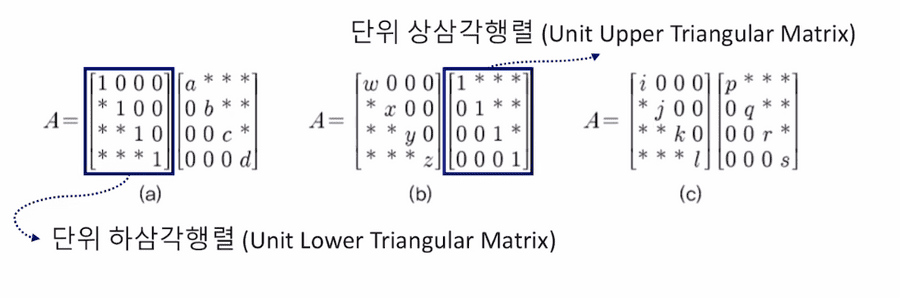 LU 분해의 형태 3가지
LU 분해의 형태 3가지
위와 같이 [1. 단위 하삼각행렬 x 상삼각행렬, 2. 하삼각행렬 x 단위상삼각행렬, 3. 하삼각 x 상삼각]의 형태로 나뉘어 진다.
ex1) A=⎣⎢⎡13228641413⎦⎥⎤=⎣⎢⎡132011001⎦⎥⎤⎣⎢⎡100220423⎦⎥⎤
ex2) B=⎣⎢⎡1−12234−320107⎦⎥⎤=⎣⎢⎡1−12010001⎦⎥⎤⎣⎢⎡100250−3−16115⎦⎥⎤
이번 시간에는 정방행렬에 대한 LU분해만 알아보자.
📌 LU 분해 가능여부
행렬 A에 대해, [1. 한 행에 0이 아닌 상수를 곱하는 연산, 2. 위쪽 행의 상수배를 다른 행에 더하는 연산] 두 개의 연산만을 통해 상삼각행렬을 만들 수 있으면 해당 행렬은 LU분해할 수 있다.
ex) A=⎣⎢⎡10000102−1⎦⎥⎤은 LU분해할 수 없다.
📌 기본행렬을 이용한 LU 분해
EnEn−1...E1A=U라 할 때 A=E1−1...En−1−1En−1U 이기 때문에
L은 E1−1...En−1−1En−1가 된다.
A=⎣⎢⎡120−11420−2⎦⎥⎤
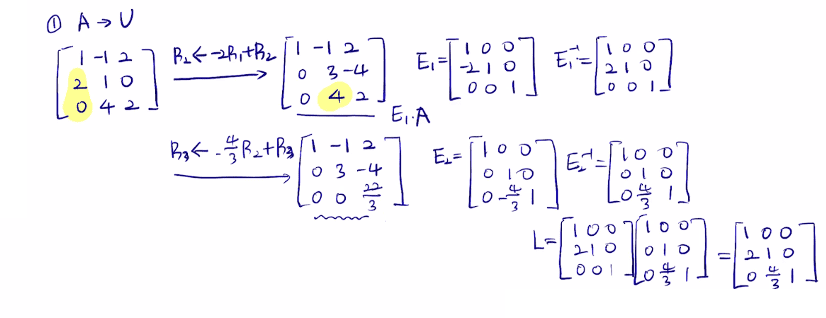 기본행렬을 이용한 LU 분해
기본행렬을 이용한 LU 분해
위의 과정을 통해 A=LU=⎣⎢⎡1200134001⎦⎥⎤⎣⎢⎡100−1302−4322⎦⎥⎤ 이다.
📌 두리틀 알고리즘을 통한 LU분해
두리틀 알고리즘을 통해 하삼각행렬과 상삼각행렬을 계산할 수 있다.
 두리틀 알고리즘
두리틀 알고리즘
이 알고리즘을 통해 A=⎣⎢⎡1112353512⎦⎥⎤을 LU분해 해보자.
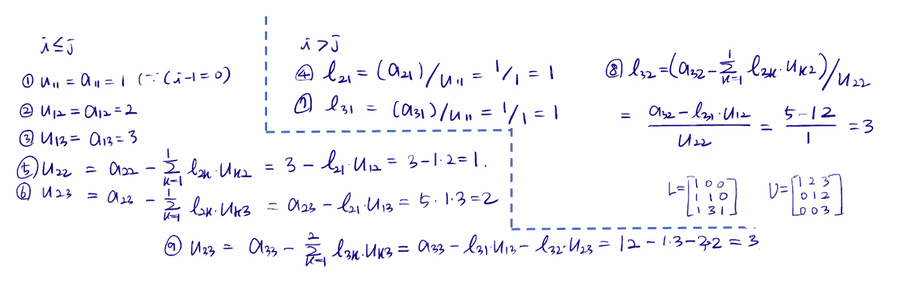 두리틀 알고리즘을 통한 LU분해
두리틀 알고리즘을 통한 LU분해
📌 LU분해의 활용
강해져서 돌아오거라
📌 LU분해를 통한 역행렬 구하기
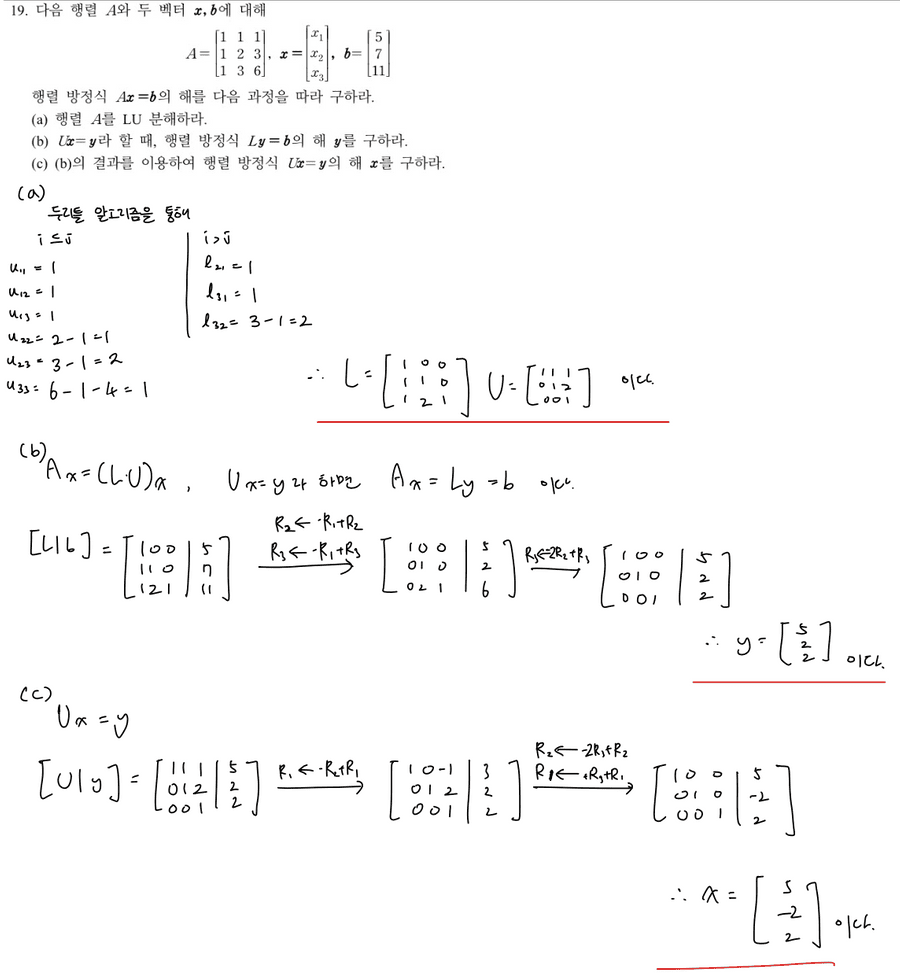 LU분해를 통해 역행렬
LU분해를 통해 역행렬
블록행렬의 역행렬
📌 블록 상삼각행렬
다음과 같은 형태를 갖는 블록행렬을 블록 상삼각행렬이라 한다.
📌 블록 상삼각행렬의 역행렬 구하기
📌 블록 대각행렬
📌 블록 대각행렬의 역행렬 구하기
📌 슈어 보수행렬
📌 슈어 보수행렬을 통해 블록행렬의 역행렬 구하기