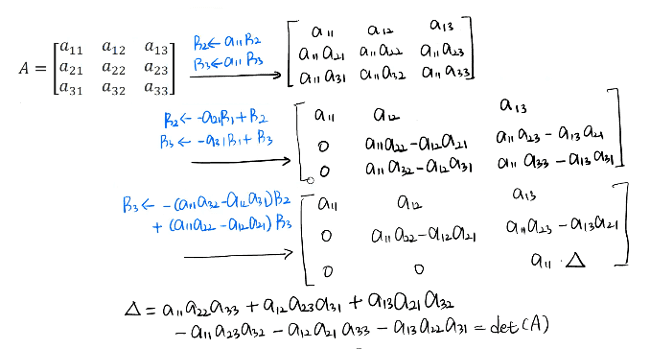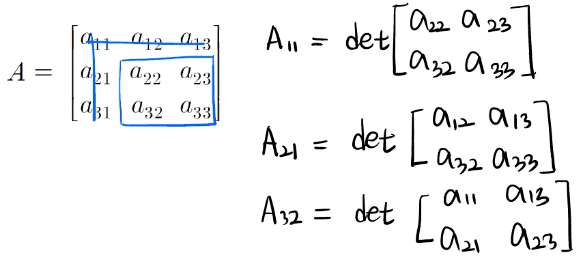Linear Algebra #05-1 | Determinants
2022년 10월 16일 13:11
Determinants
📌 Determinants
Determinants(행렬식)은 행렬을 대표하는 값으로 정방행렬 A에 대해 det(A) 또는 ∣A∣로 표기된다.
determinants는 [역행렬 존재여부 및 구할 때, 연립 선형 방정식을 풀 때, eigenvalue와 eigenvector]에 사용된다.
-
1 × 1정방행렬의 determinant
A=[a]의 det(A)=det([a])=a
-
2 × 2정방행렬의 determinant
A=[acbd]의 det(A)=det([acbd])=ad−bc
-
3 × 3정방행렬의 determinant
A=⎣⎢⎡a11a21a31a12a22a32a13a23a33⎦⎥⎤의
det(A)=
a11a22a33+a12a23a31+a13a21a32−a11a23a32−a12a21a33−a13a22a31
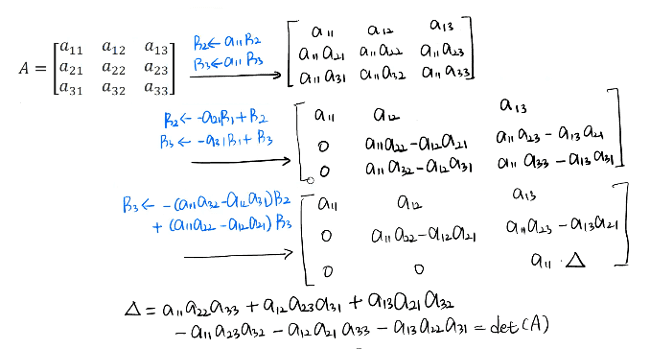 3 × 3의 determinant원리
3 × 3의 determinant원리
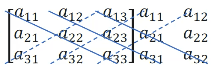 Sarrus method
Sarrus method
📌 Minor determinant
Minor determinant(소행렬식)은 어떤 aij의 요소가 있는 i번째 row와 j번째 column을 제거한 행렬의 Determinant를 말하며 Aij로 표기한다.
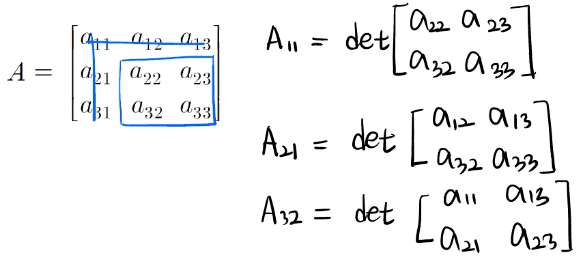 Minor determinant
Minor determinant
이 소행렬식을 이용해 행렬식을 다시 일반화 해보면
a11(a22a33−a23a32)+a12(a23a31−a21a33)+a13(a21a32−a22a31)
=a11A11−a12A12+a13A13이 된다.
만약 column을 기준으로 묶었다면 a11A11−a21A21+a31A31이 된다.
📌 Laplace Expansion
Minor determinant를 통해 n×n의 determinant를 수식화한 것을 Laplace Expansion이라고 한다.
-
행 기준
det(A)=k=1∑naik(−1)i+kAik
-
열 기준
det(A)=k=1∑nakj(−1)k+jAkj
📌 Cofactor Expansion
Cofactor Cij=(−1)i+jAij를 통해 앞의 수식을 좀 더 간결하게 나타낼 수 있다.
 Cofactor expansion
Cofactor expansion
Properties of Determinants
📌 property1
📌 property2
📌 property3
📌 property4
📌 property5
📌 property6
📌 property7
📌 property8
📌 property9
📌 property10
📌 property11
📌 property12
📌 property13
📌 property14
📌 property15