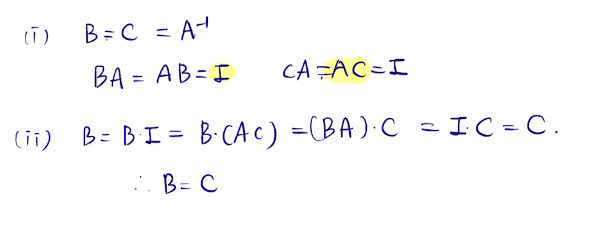yeim log

Linear Algebra #03 | Matrix

2022년 10월 01일 19:21

행렬

📌 행렬

행렬은 수나 식을 사각형 모양으로 배열하고 괄호로 묶어놓은 것을 말한다. 아래와 같이 열 벡터, 행 벡터, amna_{mn}(entry or element)로 구성되어 있다.

img
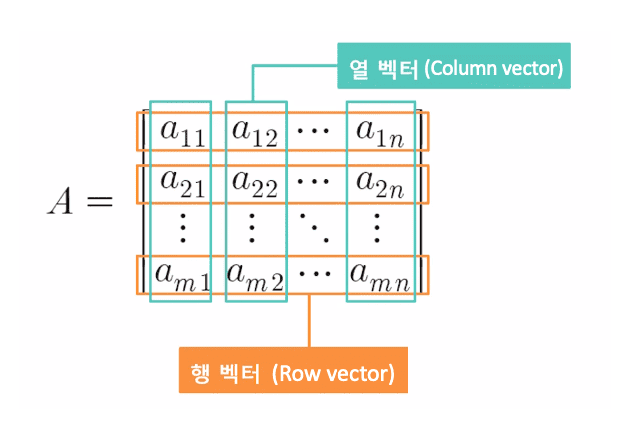행렬의 구성요소

행렬의 종류에는 정방행렬(행과 열의 개수가 같은), n차 정방행렬(행과 열의 개수가 n인 정방행렬), 단위 행렬(항등 행렬), 영행렬 등이 있고, a11, a22, ...a_{11},\ a_{22},\ ... 같이 행과 열의 번호가 같은 성분을 Main diagonal entry라고 한다.


📌 행렬의 연산

덧셈과 뺄셈은 두개의 행렬 A, B의 각 행, 열의 개수가 같아야 한다. 즉,

A=[aij]m×n, B=[bij]m×nA=[a_{ij}]_{m×n},\ B=[b_{ij}]_{m×n} 일 때 합의 각 성분들은  cij=aij+bij\ c_{ij}=a_{ij}+b_{ij}이다.


스칼라 곱은 스칼라  k\ k를 행렬 A=[aij]m×nA=[a_{ij}]_{m×n}에 곱하는 것으로, 스칼라 곱 kAkA는 kA=[kaij]m×nkA=[ka_{ij}]_{m×n}으로, AA의 각 성분을 kk배한 것이다.

행렬 곱 연산은 A의 열의 개수와 B의 행의 개수가 같을 때만 가능하다. 즉,

A=[aij]m×p, B=[bjk]p×nA=[a_{ij}]_{m×p},\ B=[b_{jk}]_{p×n} 일 때 연산이 가능하며, 결과인  AB=[cik]m×n\ AB=[c_{ik}]_{m×n}의 각 성분들은 다음과 같다.

cik=ai1b1k+ai2b2k+ ... +aipbpk=∑j=1paijbjkc_{ik}=a_{i1}b_{1k}+a_{i2}b_{2k}+\ ...\ +a_{ip}b_{pk}=\displaystyle\sum_{j=1}^p a_{ij}b_{jk}

위의 식은 앞으로 여러가지 증명할 때 사용된다. 행렬의 곱에서 주의해야 할 점은 AB≠BAAB \not= BA이라는 것이다.


📌 행렬의 특징

img
행렬의 거듭제곱
img
행렬 연산의 기본특징

역행렬

📌 역행렬

n차 정방행렬 AA에 대해  AB=BA=In\ AB=BA=I_n을 만족하는 행렬 BB를 행렬 AA의 역행렬 이라 하며,  A−1\ A^{-1}로 나타낸다.

역행렬이 존재하는 행렬을 가역(invertible)이라 하고, 그렇지 않을 때는 비가역 행렬(noninvertable)이라 한다.

가역이라면 A의 역행렬은 유일하다.

img
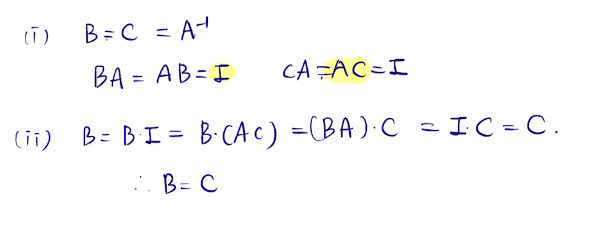역행렬의 유일성

A−1A^{-1}이 B와 C 두개가 있다고 할 때 위의 식을 통해서 B와 C가 같다는 것을 확인할 수 있다.


📌 2x2의 역행렬

A=[abcd]A = \begin{bmatrix}a&b \\ c&d\end{bmatrix} 에 대하여 ad−bc≠0ad - bc \not= 0이면,

역행렬은 A−1=1ad−bc[d−b−ca]A^{-1}=\dfrac1{ad-bc}\begin{bmatrix}d&{-b} \\ {-c}&a\end{bmatrix}이다.


📌 역행렬의 성질

n차 정방행렬 A, B가 가역이고, αα는 0이 아닌 스칼라리 때, 다음의 성질을 만족한다.

(1) A−1A^{-1}는 가역이고, (A−1)−1=A(A^{-1})^{-1} = A이다.

(2) ABAB는 가역이고, (AB)−1=B−1A−1(AB)^{-1} = B^{-1}A^{-1}이다.

(3) αAαA는 가역이고, (αA)−1=1αA−1(αA)^{-1} = \dfrac1αA^{-1}이다.

(4) AkA^k는 가역이고, (A−1)k=(Ak)−1(A^{-1})^k = (A^k)^{-1}이다. (k는 0 이상의 정수)


특수한 행렬

📌 전치행렬

행렬 A=[aij]m×nA = [a_{ij}]_{m×n}의 행과 열을 바꾸어 놓은 행렬을 전치행렬이라 하고, A⊺A^{\intercal}로 나타낸다.

전치행렬 A⊺=[aij′]n×mA^{\intercal}=[a'_{ij}]_{n×m}의 성분 aij′a'_{ij}는 AA의 ajia_{ji}와 같다.


행렬 A, BA,\ B와 스칼라 αα에 대해 다음의 성질이 성립한다.

(1) (A⊺)⊺=A(A^{\intercal})^{\intercal} = A

(2) (A+B)⊺=A⊺+B⊺(A+B)^{\intercal} = A^{\intercal} + B^{\intercal}

(3) (AB)⊺=B⊺A⊺(AB)^{\intercal} = B^{\intercal}A^{\intercal}

(4) (αA)⊺=αA⊺(αA)^{\intercal} = αA^{\intercal}

(5) AA가 가역이면, (A⊺)−1=(A−1)⊺(A^{\intercal})^{-1} = (A^{-1})^{\intercal}이다.


📌 대칭행렬과 반대칭행렬

정방행렬 AA가 자신의 전치행렬 A⊺A^{\intercal}와 같으면 AA를 대칭행렬(symetric matrix)이라고 한다.

정방행렬 AA가 자신의 전치행렬의 음수 −A⊺-A^{\intercal}와 같으면 AA를 반대칭행렬(skew-symetric matrix)이라고 한다.

정방행렬과 전치행렬의 합과 차를 통해 아래처럼 대칭/반대칭행렬을 만들 수가 있다.

img
대칭/반대칭 행렬 만들기

📌 대각행렬

주대각 성분 이외의 성분이 모두 0인 정방행렬을 대각행렬(diagonal matrix)이라 한다. 주대각 성분이 a11, a22, ..., anna_{11},\ a_{22},\ ...,\ a_{nn}인 n차 대각행렬은 diag(a11, a22, ..., ann)diag(a_{11},\ a_{22},\ ...,\ a_{nn})으로 표기한다.


📌 대각합(Trace)

정방행렬 A=[aij]n×nA = [a_{ij}]_{n×n}의 대각합 tr(A)tr(A)는 주대각 성분의 합이다.

tr(A)=a11+a22+ ... +anntr(A) = a_{11}+a_{22}+\ ...\ +a_{nn}


(1) n차 정방행렬 A,BA,B에 대해, tr(A+B)=tr(A)+tr(B)tr(A+B) = tr(A)+tr(B)이다.

(2) n차 정방행렬 AA와 스칼라 cc에 대해, tr(cA)=c⋅tr(A)tr(cA) = c\cdot tr(A)이다.

(3) n×mn×m 행렬 AA와 m×nm×n 행렬 BB에 대해, tr(AB)=tr(BA)tr(AB) = tr(BA)이다.

(4) n차 정방행렬 A,B,CA,B,C에 대해, tr(ABC)=tr(CAB)=tr(BCA)tr(ABC) = tr(CAB) = tr(BCA)이다.


📌 삼각행렬(Triangular matrix)

주대각 성분 아래쪽의 모든 성분이 0인 정방행렬을 상삼각행렬이라 하고,

주대각 성분 위쪽의 모든 성분이 0인 정방행렬을 하삼각행렬이라 한다.

img
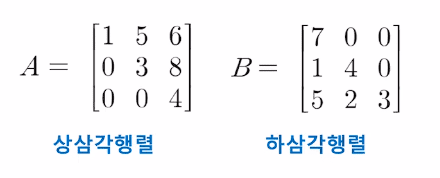삼각행렬

상삼각행렬 Un=[uij]n×nU_n=[u_{ij}]_{n×n}에서 i>ji>j이면 uij=0u_{ij}=0이다.

하삼각행렬 Ln=[lij]n×nL_n=[l_{ij}]_{n×n}에서 i<ji<j이면 lij=0l_{ij}=0이다.


상삼각행렬끼리 곱하면 상삼각행렬, 하삼각행렬끼리 곱하면 하삼각행렬이 된다.


📌 블록행렬(Block matrix)

행렬의 특정 행과 열 사이를 경계로 나누어 부분행렬로 표현한 것을 블록행렬(구획행렬)이라 한다.

  • 합: 크기가 서로 같은 행렬 AA와 BB가 동일한 방법으로 분할한 블록행렬인 경우, 대응되는 부분행렬들 간의 합을 통해 계산 가능하다.
  • 스칼라곱: 블록행렬AA에 스칼라 cc를 곱하는 것은 각 부분행렬에 cc를 스칼라곱 한 것과 같다.

  • 곱: A, B에 대응하는 AijA_{ij}의 열의 개수와 BjkB_{jk}의 행의 개수가 일치할 때, 두 행렬의 곱 C=ABC=AB를 계산할 수 있다.

    Cik=∑jAijBjkC_{ik} = \displaystyle\sum_j A_{ij}B_{jk}