Linear Algebra #02 | Linear Equation

2022년 09월 18일 21:21

연립 선형 방정식

아래와 같이 최고차수가 1인 형태의 방정식을 선형 방정식이라 한다.

$a_1x_1 + a_2x_2 + ... + a_nx_n = b$

좀 더 자세히 보면 $x_1, x_2, ..., x_n$ 부분의 variables (or unknowns)와 $a_1, a_2, ..., a_n, b$ 부분의 coefficients(a는 계수, b는 상수)로 이루어져 있다.

variable의 개수에 따라 달라지는데 2개인 경우 2차원의 평면에서 직선, 3개인 경우 3차원 공간에서 평면, 4개 이상의 경우 표현될 수 없는 hyperplane이라 표현한다.

동일한 미지수를 갖는 1개 이상의 선형방정식들의 집합을 연립 선형 방정식이라 한다.

이 때 모든 선형 방정식을 만족하는 미지수의 값을 solution(해)라고 하며 여러개일 경우 solution set이라 한다.

선형 방정식은 유일한 해를 갖는데, 아래의 그래프처럼 무수히 많거나, 해가 없기도 하다.

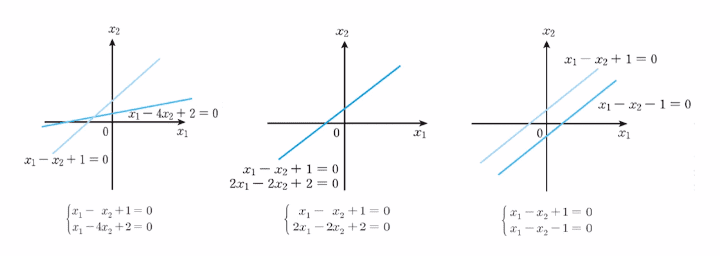
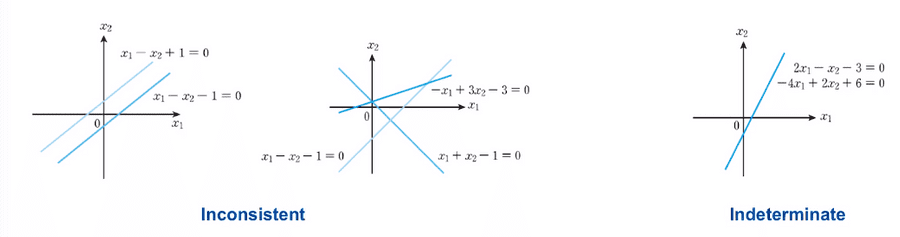
해가 존재하지 않는 경우는 inconsitent(모순) 또는 impossible(불능)이라고 한다.

해가 무수히 많은 경우는 indeterminate(부정) 이라고 한다.

두개의 연립 선형 방정식이 동일한 해 집합을 갖는 것을 동치 연립 선형 방정식(Equivalent systems of linear equations) 이라 한다.

하나의 연립 선형 방정식으로 동연선방을 만드는 방법은 아래의 3가지 방법을 이용할 수 있다.

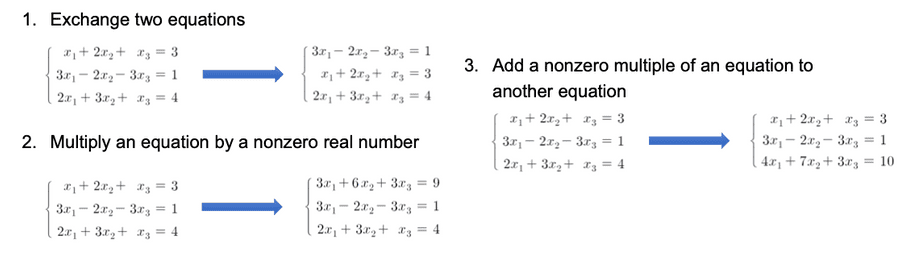
순서변경

상수 곱하기

같은 연선방 내의 선방 더하기

$\begin{cases} &x_1 + 2x_2 = 5 &(1) \\ &2x_1 + 3x_2 = 8 &(2)\end{cases}$

(1)에서 $x_1 = 5 - 2 x_2$ 로 하고 (2)의 $x_1$ 에 대입하는 Substitution방법을 주로 사용해왔지만 소거법(Elimination method)이라는 것을 사용할 것이다.

연립 선형 방정식을 아래와 같이 행렬로 나타낼 수 있다. A를 Coefficient matrix(계수행렬)라 하고, b를 Constant vector(상수벡터)라 하고 행렬 방정식(Matrix equation)이라고 한다.

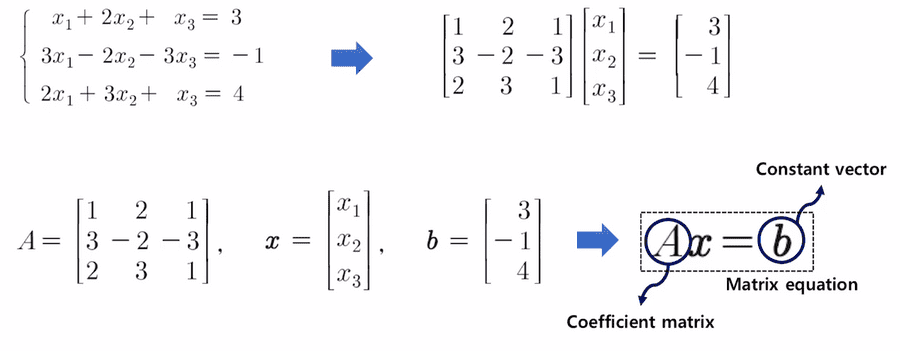
각 선형 방정식이 행렬 방정식에서 Row로 표현되어 있기 때문에 행렬 방정식에서 동연선방을 만드는 방법을 Elementary Row Operations(ERO) 라고 부른다.

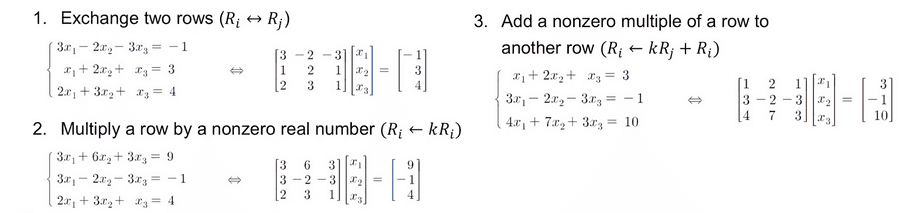
위와 같이 연립 선형 방정식에서 동연선방을 만드는 방식과 동일하다.

나중에 Gauss-Jordan 소거법에서 ERO 연산을 많이 할 것이기 때문에 간소화한 행렬 방정식을 Augmented matrix(첨가 행렬)이라 한다.

각 row에서 첫번째로 0이 아닌 지점을 pivot-entry라고 하는데 아래 3가지 조건을 만족하는 행렬 방정식을 REF matrix라고 한다. (사다리꼴 모양)

0으로만 이루어진 행은 항상 맨 아래에 있어야 한다.

아래에 있는 pivot-entry는 무조건 오른쪽에 있어야 한다.

pivot은 항상 1이어야하고 아래는 다 0이어야 한다.

REF matrix에서 각 column의 pivot을 제외하고 나머지가 모두 0인 행렬을 RREF matrix라고 한다.